Origin of the Coral Trait

We boa breeders often wish to be able to "prove" whether or not a boa that may possess the gene for a particular trait actually does possess that gene, or not. Sometimes this is a simple exercise: if an Albino or het-Albino boa is bred to a 66% possible het-Albino boa and at least one albino baby is produced, we then know that the 66% possible het-Albino is het-Albino. In this case we have proven that the possible het-Albino is in fact a het-Albino. But what happens when such a pairing produces a litter of, say, 15 babies of which none are albino? Many would be tempted to conclude that they have proven that the possible het-Albino is not het-Albino, but this conclusion would be incorrect - we must remember the old adage, "You can't prove a negative." What this means is that even if this pairing produces 100 babies over the course of several breeding seasons and produces no albinos, there is still a chance that the possible het-Albino is indeed het-Albino and that the failure to produce an albino in all of those babies is simply a result of very bad luck - it is a very unlikely outcome, but it CAN happen, just as it is extremely unlikely that you will match all of the Super Lottery numbers, yet somebody always does eventually.

This RLT Ghost het-Albino is a possible Super Hypo

We will have to breed her and apply statistics to find out whether she more likely is or is not!

So if we can't prove that a possible het-Albino is not het-Albino, for example, no matter how many non-albino babies we produce, then what can we do? The best we can do is to show that it is statistically very unlikely that the possible het-Albino is a het-Albino, and to do that we need to know a little bit about statistics. Also note that this type of statistical evaluation applies not just to possible het-Albinos but to possible heterozygotes (possible hets) for any simple recessive trait (Anery Type I, Anery Type II, Black-Eyed Anery, Blood, BWC, VPI T+, etc....), and can also be used to similarly evaluate how likely it is that a possible Super (homozygote) for a simple dominant trait (or a co-dominant/incompletely dominant trait where the heterozygous form is not visually distinguishable from the homozygous "Super" form 100% of the time, for example, the Hypo trait) actually is a Super.

Rolling 3 aces has a probability of just 1 in 216, but you can likely do it in 20 minutes or less.

In the example above, it turns out that the probability of a litter of 15 babies from a het-Albino X het-Albino breeding having zero albinos is over 1.3 percent (better than 1 in 100) - certainly bad luck in not having produced any albinos in those 15 babies, but not astronomically bad. To put this into perspective, here's a little experiment you can easily perform. The probability of rolling three 6-sided dice and getting three aces (ones) is only 1 in 216, or about 0.46 percent. Yet if you start rolling your three dice, you will eventually get that 1-1-1 result. It may occur on the first roll, or it may take you 100, 200, 300 or more rolls, but eventually it will happen, and assuming that you can roll about 12 times per minute, you will most likely get that 1-1-1 result in less than 20 minutes. So that 0.46 percent probability really isn't all that unlikely, is it? Now consider that the litter outcome above is nearly 3 times more likely to occur than that 1-1-1 roll of the dice!

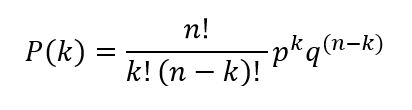
where:

P(k) = the probability of k successes in n trials

k = the number of successful results

n = the number of trials

p = the probability of success in any one trial

q = (1-p) = the probability of failure in any one trial (getting any outcome other than the one of interest)

n! = 1 x 2 x 3 x...x n. Though this equation may look a bit intimidating, it is actually quite easy to plug into a spreadsheet to perform the calculations and view the results graphically as we will do in the following example to demonstrate its usefulness. If you are nevertheless having bad math class flashbacks, just hang in there a little longer - the math gets easier soon!

Leaving our issue about possible het-Albinos behind for the moment, imagine that we have a female het-Albino that was bred by a male het-Albino and we are interested in how many albino babies we are likely to get in a litter of, say, 20 babies. From our understanding of basic genetics, we know that albinism is a simple recessive trait and that when breeding het-Albino X het-Albino we would expect 1 in 4 babies (¼) to be albino. So we can easily say that in a litter of 20 babies, we would on average expect 5 of those babies to be albino (¼ x 20 = 5). While this very simple calculation does correctly give us the "expected" or "most likely" result, it tells us nothing about the likelihood of this result relative to other possible results (other numbers of albino babies). That's where the binomial distribution comes in. In this example, our variables would be:

k = the number of successful results (k = number of albino babies)

n = the number of trials (n = 20 babies)

p = the probability of success in any one trial (the probability that a given baby will be albino = p = ¼ = 0.25)
q = the probability of failure in any one trial (the probability that a given baby will not be albino = (1-p) = ¾ = 0.75)

To develop the probability distribution, we solve the binomial distribution equation for each possible number of albino babies k that could occur in the litter (0, 1, 2,..., 20). This is where the spreadsheet comes in really handy - solving the equation 21 times on a calculator is no fun! In spreadsheet form, our solutions look like this:

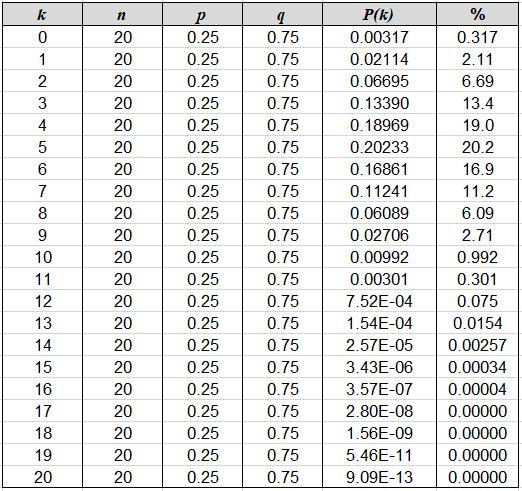
The percent column above simply shows P(k) as a percentage; for example, we can see that our "expected" outcome of 5 albino babies, although it is the most likely result, will actually occur only about 20.2 percent of the time. Graphing these results creates a powerful summary that is easily understood:

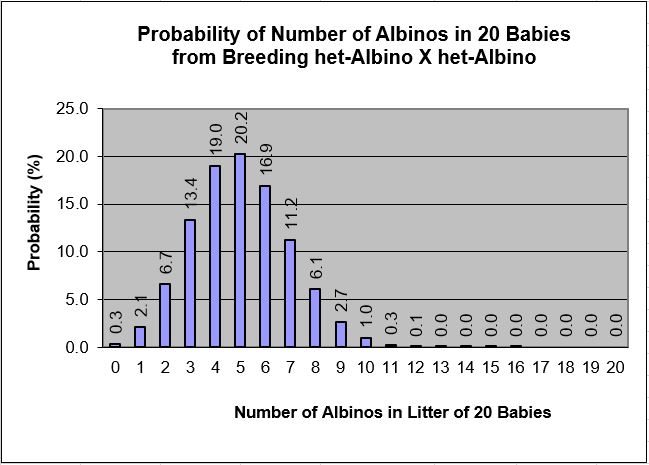
Here we can quickly see that the probability of getting 10 albino babies in this litter of 20 is only about 1 percent (1 in 100), and the probability of getting more than 12 albinos quickly becomes astronomically small (the values in the graph are rounded off to one decimal place, but you can see the values in the table above). At the opposite end of the spectrum, the probability of getting zero albino babies in our litter of 20 is only about 0.3 percent, or about 3 in 1,000. The table and graph above provide much more insight into the range and likelihood of possible results one might expect from this breeding than did the simple "expected" or "most likely" estimate of 5 albinos.

Producing just one albino baby proves that a possible het-Albino is het-Albino.

As stated previously, it cannot be proven that a possible het is not a het, but we can demonstrate through the binomial distribution that it is increasingly unlikely with greater and greater numbers of non-homozygous offspring produced (for example, greater and greater numbers of non-albino offspring from a possible het-Albino bred to het-Albinos or Albinos). Of course, if during any breeding trial the possible het-Albino does produce an albino - even just one - then that possible het-Albino is proven once and for all to be a het-Albino (a rare exception would be if a het-Albino female bred by a possible het-Albino male produced an albino baby via parthenogenesis whereby some or all babies in a litter have genetic material only from their mother, but this is uncommon and beyond the scope of this discussion).

The particular case we are interested in from the example above is that of zero Albino babies produced, which translates to zero successful results (k=0). Using the binomial distribution equation, we could calculate the probability of k=0 occurring for increasing numbers of offspring n to develop a table similar to the one above. However, as we are not interested in the probability distribution of potential results in this case, only the case of k=0, there is a simpler mathematical shortcut. If q is the probability of failure in a given trial as defined above, and n is the total number of trials (babies produced), then the probability of there being no successful trials (no albino babies) is described by:

We promised you easier math, and there it is! In a het-Albino X het-Albino breeding, the probability of any given baby being a non-Albino (i.e., the probability of failure, q) is 3 in 4 (¾ or 0.75) as we saw above. With our example litter of 20 babies from above, we would have (¾)²⁰ = 0.00317 or 0.317 percent, exactly the same result that we got using the binomial distribution equation with k=0 and n=20 in the table above!

66% possible het-Albino Middle Mama's litter of

45 non-Albino babies showed her to not be het-Albino with a certainty of 99.9998%.

What the result of this example tells us is that if we were breeding two het-Albinos together and got a litter of 20 babies, the probability of producing zero Albino babies is only about 0.3 percent, or about 3 in 1,000. However, because one of our breeder boas is actually a possible het-Albino, this result suggests that the possible het-Albino is not a het-Albino - it does not prove it, but it tells us that this would be a very unlikely result if the possible het-Albino is het-Albino.

On the basis of these results, we can essentially say that the probability of our possible het-Albino actually being a het-Albino is equivalent to the probability of the breeding results - only about 3 in 1,000 or 0.3 percent. To put it another way, we can essentially say that our possible het-Albino is not het-Albino with a certainty of about 997 in 1,000 or 99.7 percent. These latter two statements may not be completely correct in the strictest statistical/mathematical sense, but for larger values of n where P(k=0) becomes small these statements become valid (such statements may not apply precisely when n is very small; for example, if your 66% possible het-albino was bred by a het-Albino produces a litter of mostly slugs and just 3 babies of which none are albino, it does not mean that you should start calling your 66% possible het-Albino a 42% possible het-Albino [see table above]).

The 99.9998% certainty provided by 45 non-Albinos

from a het X poss het breeding is achieved with just 16 non-Albinos from Albino X poss het.

Note that we can also easily apply these equations to breedings of Albino to possible het-Albino (or any recessive homozygote to possible heterozygote). In these cases, p=½ and q=(1-p)=½. As one would expect, the probability of k=0 decreases more quickly as n increases for the homozygote X possible het case than it does for the het X possible het case. In similar fashion, for a simple dominant trait or a co-dominant/incompletely dominant trait where the heterozygous form is not visually distinguishable from the homozygous "Super" form 100% of the time, such as for the Hypo trait, one can evaluate a possible Super Hypo (possible homozygous Hypo) by breeding it to a non-Hypo, for example, and doing the calculations for a heterozygous Hypo [p=½ and q=(1-p)=½]. As the number n of Hypo babies produced increases without a normal (non-Hypo) baby being produced, the probability of the possible Super Hypo actually being a Super Hypo likewise increases.

Note that in all of these cases it does not matter whether a possible het is 66% possible or 50% possible, or if a possible Super is 50% possible or 33% possible, for example. These probabilities arise from the breedings that produced them (e.g. a het-Albino bred to a normal boa to produce a 50% possible het-Albino); the statistical evaluation of offspring described above is a completely separate probability calculation. These two probabilities cannot be combined by simple multiplication because they do not represent independent trials; whereas one baby boa's genetic makeup has no influence on the next baby boa's genetic makeup (much the same way that the outcome of a coin flip has no effect on the outcome of the next coin flip), if a boa that is 50% possible het-Albino by birth is not het-Albino, for example, then the outcome of that "first trial" has already determined the outcome of all of the subsequent trials (albino babies have zero probability of being produced). The potential influence of the first trial on the subsequent trials means that the trials are not independent, and therefore the combined probability for these trials is not represented by the binomial distribution; i.e., we cannot combine the "probability by birth" with the probability based on the offspring evaluation.

However, we are able to, for example, combine the probabilities calculated for a possible het-Albino that has been bred to both Albinos and het-Albinos by simple multiplication because these are independent trials. So, if the breeding to the het-Albino produced 12 babies with no albinos [P(k=0) = (¾)¹² = 0.03168 = 3.2%], and the breeding to the Albino produced 8 babies with no albinos [P(k=0) = (½)⁸ = 0.003906 = 0.39%], the combined probability of these results is found by multiplying the probabilities together: (¾)¹² x (½)⁸ = 0.03168 x 0.003906 = 0.0001237 = 0.012%, or a bit over 1 in 10,000.

It is up to each individual to decide whether he or she is sufficiently convinced that a possible het is not a het based on the statistics. There is no magic number - there is no requirement that the probability of a possible het actually being a het be less than 1 in 100, or less than 1 in a million before you can call the possible het "not a het." In most cases, it isn't critical because the majority of the time it is just a matter of a breeder obtaining a possible het that they hope has that gene for the trait that they want to produce, and it turns out that the boa has it or it doesn't without much consequence either way. However, consider the following case study which provides an example of when the evaluation of a possible het-Albino was critically important!